
یکی از توزیع های ویژه ای که از توزیع نرمال به دست می آید، توزیع t استیودنت است. استیودنت نام مستعار پروفسور W. S. Gosset است. اجازه دهید انتگرال قطعی توزیع احتمال نرمال را در نظر بگیریم که در آن انحرافات بر حسب انحراف معیار جمعیت آن بیان شده است.
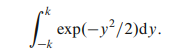
انتگرال نشان دهنده مساحت تحت پوشش توزیع نرمال بین حدود K تا -K است،
اگر
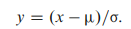
انتگرال نشان دهنده احتمال تجمعی برای x در بین حدها است
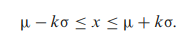
در اینجا میانگین و انحراف معیار توزیع نرمال است. معمولاً انحراف معیار مشخص نیست. این تخمین انحراف معیار s از تعداد محدود مشاهدات است که مشخص است.
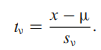
v نماد درجه آزادی متغیر Tv است.
روش دیگر برای تعریف متغیر توزیع t استیودنت به شرح زیر است:
اگر X یک متغیر نرمال (0، 1) و Y یک متغیر X2 باشد، T Student نیز
تعریف میشود:
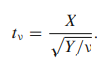
اثبات برابری آنها به شرح زیر است:
طبق تعریف
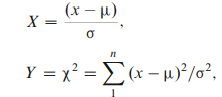

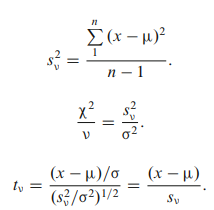
حال اگر بخواهیم احتمال آن را دریابیم
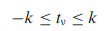
یا عبارت جایگزین آن، احتمال
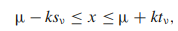
سپس احتمال تجمعی مورد نیاز دیگر ت داده نمی شود، بلکه توسط انتگرال داده می شود
تابع چگالی t استیودنت

یا تابع چگالی احتمال
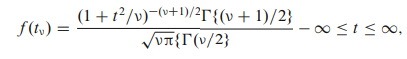
در جایی که
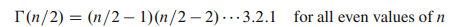
و
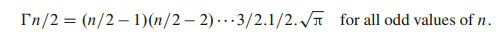
فرمول بازگشت برای تابع گاما n=2

این توزیع برای نمونه های کوچک مفید است.
میانگین و واریانس توزیع t استیودنت
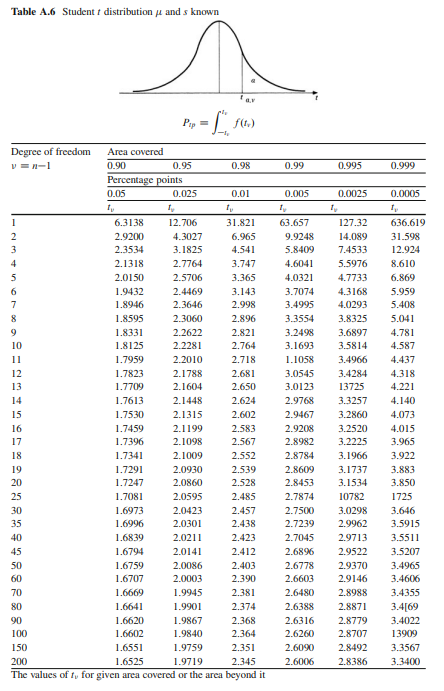
میانگین توزیع صفر است. انحراف معیار v/v-2 است. مقدار v بزرگتر از 2 است. توزیع در حدود t=0 متقارن است. بدیهی است که با نزدیک شدن به یک عدد بزرگتر، به توزیع نرمال استاندارد تمایل دارد. توزیع t Student در شکل زیر نشان داده شده است. مقادیر آماره t برای مقادیر مختلف درجات آزادی و احتمالات در جدول زیر آورده شده است.
مقایسه توزیع نرمال و t
شکل زیر را با نمودار توزیع نرمال با انحراف معیار برابر نشان می دهد. خاطرنشان می شود که توزیع t دارای احتمال نسبتاً بیشتری است که در دنباله های آن متمرکز شده است. مانند توزیع نرمال متقارن، پیوسته و زنگوله ای است و با افزایش n یا به سرعت به توزیع نرمال همگرا می شود.

کاربرد t-Statistic
1-برای آزمون میانگین نمونه، در صورتی که تفاوت معنی داری با میانگین جامعه داشته باشد. در این مورد میانگین جمعیت مشخص است که در برخی موارد ممکن است میانگین حاصل از آزمایشگاههای مختلف یا میانگین متحرک ویژگی یک قلم باشد که در فواصل دورهای اندازهگیری میشود. در این مورد فرض می کنیم که ویژگی قلم با گذشت زمان و شرایط محیطی یا شناخته شده تغییر نمی کند.
روابط بین ویژگی و زمان یا شرایط محیطی وجود دارد. به عنوان مثال، مقدار مقاومت نیکل کروم با زمان تغییر می کند و جرم سیلندر پلاتین ایریدیوم پس از تمیز کردن در بخار با زمان تغییر می کند. سپس اصلاحات لازم برای میانگین متحرک اعمال می شود.
2-برای آزمون تفاوت بین دو میانگین نمونه. این کار برای ارزیابی کیفیت نتایج آزمون بهدستآمده توسط ناظران مختلف یک آزمایشگاه یا نتایج بهدستآمده از آزمایشگاههای مختلف در یک آزمون مفید است.
3-برای آزمون اهمیت یک ضریب همبستگی نمونه مشاهده شده و ضریب رگرسیون نمونه.
4-برای آزمون معنی داری ضرایب همبستگی جزئی مشاهده شده.
منبع توزیع احتمال مثلثی:عدم قطعیت اندازه گیری
