آزمون مربع خی

آزمون مربع خی فراوانی ها را مورد بررسی قرار می دهد.، یعنی تعداد دفعاتی که رخداد معینی اتفاق می افتد. برای مثال جدید زیر فراوانی های مقادیر مختلف بدست آمده برای غلظت یون نیترات را هنگام انجام 50 اندازه گیری بر روی یک نمونه می باشد.

این گونه اندازه گیری ها معمولا فرض می شود که از یک جمعیت با توزیع طبیعی بدست آمده اند، آزمون مربع خی می تواند برای بررسی متفاوت بودن معنی دار فراوانی های مشاهده شده از آنچه که در حالت قبول فرض صفر انتظار می رفت، بکار رود:

برای بررسی اینکه آیا فراوانی های مشاهده شده، O_i، با فراوانی های مورد انتظار، E_i، بر اساس فرض صفر مطابقت دارد یا نه، آماره X₂ حساب می شود:

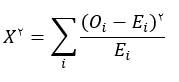
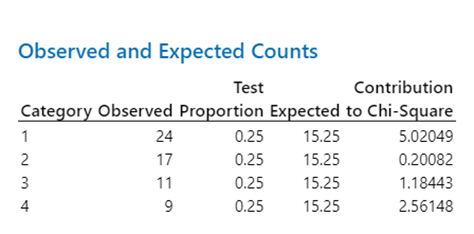
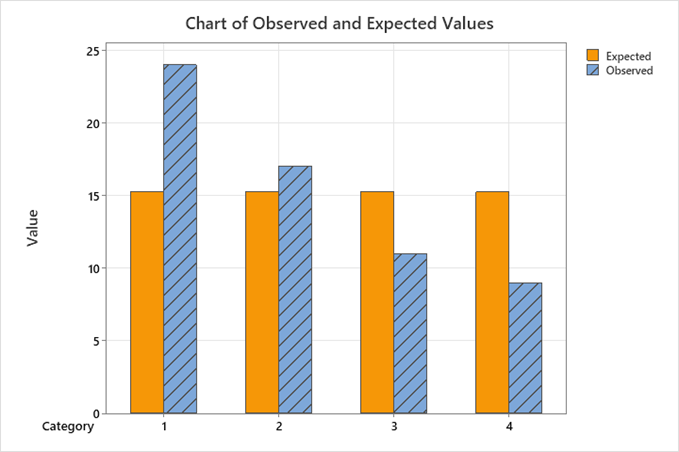
مثال27: تعداد شیشه های شکسته شده گزارش شده توسط کارکنان چهار آزمایشگاه در طول دوره ای معین در زیر نشان داده شده است. آیا دلیلی بر متفاوت بودن اعتماد پذیری کارکنان وجود دارد؟

تعداد شکست ها

24

17

11

9

قبول فرض صفر به این معنی است که تفاوتی در اعتماد پذیری کارکنان وجود ندارد. با فرض اینکه کارگران،  برای مدتی یکسان از آزمایشگاه استفاده می کنند، تعداد شکست یکسانی را برای هر کارگر، بر اساس فرض صفر، انتظار خواهیم داشت.

از آنجا که تعداد کل شکست ها 61 است، تعداد شکست مورد انتظار برای هر کارگر برابر است با:15.25=4/61 . واضح است که در عمل، داشتن تعداد همچین توزیعی غیر ممکن و تنها یک مفهوم ریاضی است. نزدیک ترین توزیع برابر عملی، در یک آرایش 15، 15، 15، 16 می باشد. سوالی که باید جواب داده شود این است که آیا اختلاف بین فراوانی های مشاهده شده  و مورد انتظار آن چنان بزرگ است که فرض صفر  باید طرد شود؟

محاسبات مربع خی در جدول زیر نمایش داده شده است.

فراوانی مشاهده شده، O	فراوانی مورد انتظار، E	O-E	(O-E)2-E
24	15.25	8.75	5.020
17	15.25	1.75	0.201
11	15.25	4.25-	1.184
9	15.25	6.25-	2.561
جمع	61	00	X2=8.966

چنانچه مقدار X² از مقدار معینی تجاوز کند، فرض صفر طرد می شود. مقدار بحرانی، همانند دیگر آزمون های معنی دار بودن، تابع سطح معنی دار بودن آزمون و تعداد درجات آزادی است، بنابراین تعداد درجات آزادی 4-1=3 است. مقدار بحرانی برای X²  در (P=0.05)  از جدول پیوست برای 3 درجه آزادی 7.81 است. چون مقدار محاسبه شده X² بزرگتراز این مقدار است، بنابراین فرض صفر در سطح معناداری 5 درصد طرد می شود، بدیهی است کارکنان در اعتماد پذیری با هم اختلاف دارند.

یادآور می شود در این مثال آزمون t نمی تواند بکار برود، زیرا با فراوانی ها سرو کار داریم نه با متغیرهای تصادفی پیوسته)

آزمون مربع خی با استفاده از مینی تب

1. ابتدا داده ها را در یک ستون وارد مي کنيم.
2. Stat > tables > chi square goodness of fit test (one variable) 
3. )     .در قسمت observed count ،ستون مقادير مشاهدات را وارد مي کنيم.
4. دکمه ok را مي زنيم.