
عدم قطعیت نوع A و نوع B ارزیابی مولفه های عدم قطعیت
مقدمه
عدم قطعیت نوع A و نوع B دو عنصری هستند که معمولاً در برآورد عدم قطعیت اندازه گیری مورد بحث قرار می گیرند.
نوع عدم قطعیت در اکثر راهنماهای عدم قطعیت اندازه گیری و دوره های آموزشی عدم قطعیت پوشش داده شده است. ارزیابان بودجه های عدم قطعیت را بررسی می کنند تا مطمئن شوند که اجزا به درستی طبقه بندی شده اند.
با این حال، آیا تا به حال به بیشتر اطلاعات منتشر شده در مورد عدم قطعیت نوع A و نوع B نگاه کرده اید؟
هیچ کس موضوع نوع عدم قطعیت را به خوبی GUM پوشش نمی دهد. اطلاعات بسیار زیادی از راهنما ها و آموزش های دیگر حذف شده است.
ممکن است به این دلیل باشد که اکثر مردم عدم قطعیت نوع B را فقط با توزیع مستطیلی ارزیابی می کنند که گزینه های بسیار واقعی تری نیز وجود دارد.
چرا سایر گزینه ها حذف می شوند؟
در این راهنما، من قصد دارم همه چیز را در مورد عدم قطعیت نوع A و نوع B همانطور که در GUM توضیح داده شده است، به شما آموزش دهم. با این حال، من به روشی توضیح خواهم داد که نیازی به داشتن مدرک دکترا نداشته باشید.
بنابراین، اگر می خواهید نحوه محاسبه عدم قطعیت را یاد بگیرید، حتماً این راهنما را بخوانید تا همه چیزهایی را که باید در مورد عدم قطعیت نوع A و نوع B بدانید، بخوانید.
زمینه
قبل از اینکه در مورد طبقه بندی نوع عدم قطعیت بیاموزید، ایده خوبی است که درباره علت وجود آنها و اینکه از کجا آمده اند بیشتر بدانید.
در سال 1980، توصیه نامه CIPM INC-1 پیشنهاد کرد که اجزای عدم قطعیت اندازه گیری باید به دو دسته گروه بندی شوند. نوع A و نوع B.
در زیر تعریفی از واژه نامه اندازه شناسی آمده است.
در توصیه نامه CIPM INC-1 (1980) در مورد بیانیه عدم قطعیت ها، پیشنهاد شده است که مؤلفه های عدم قطعیت اندازه گیری با توجه به اینکه آیا آنها با روش های آماری ارزیابی شده اند یا موارد دیگر باید به دو دسته نوع A و نوع B گروه بندی شوند، . و این که آنها برای به دست آوردن یک واریانس مطابق با قواعد نظریه احتمالات ریاضی با استفاده از اجزای نوع B بر حسب واریانس ترکیب شوند. انحراف استاندارد حاصل بیانی از عدم قطعیت اندازه گیری است. دیدگاهی از رویکرد عدم قطعیت در راهنمای بیان عدم قطعیت در اندازه گیری (GUM) (1993، تصحیح و تجدید چاپ در سال 1995) به تفصیل ارائه شد که بر برآورد ریاضی عدم قطعیت اندازه گیری از طریق یک مدل اندازه گیری صریح با این فرض که اندازه گیری را می توان با یک ارزش اساسا منحصر به فرد مشخص کرد. علاوه بر این، در GUM و همچنین در اسناد IEC، راهنمایی در مورد رویکرد عدم قطعیت در مورد یک بار خواندن یک ابزار کالیبره شده، وضعیتی که معمولاً در اندازه شناسی صنعتی وجود دارد، ارائه شده است.
همانطور که می بینید، VIM توضیحات عالی ارائه می دهد و توصیه می کند برای جزئیات بیشتر، GUM را مطالعه کنید.
در اینجا بیانی از راهنمای بیان عدم قطعیت در اندازه گیری آمده است.
«3.3.4 هدف از طبقه بندی نوع A و نوع B نشان دادن دو روش مختلف برای ارزیابی مؤلفههای عدم قطعیت است و فقط برای راحتی بحث است. منظور از طبقه بندی این نیست که نشان دهد تفاوتی در ماهیت مؤلفه های حاصل از این دو نوع ارزیابی وجود دارد. هر دو نوع ارزیابی بر اساس توزیع های احتمال (C.2.3) هستند، و مولفه های عدم قطعیت ناشی از هر یک از انواع آن با واریانس یا انحراف استاندارد کمی می شوند. – JCGM 100
برای اطلاعات بیشتر در مورد توصیه نامه CIPM INC-1 (1980)، به iso.org مراجعه کنید. متن به زبان فرانسوی است اما با ابزارهایی مانند Google Translate به راحتی قابل ترجمه است.
اکنون که VIM و GUM را خوانده اید، می توانید درک کنید که استفاده از انواع عدم قطعیت (به عنوان مثال A & B) به شما کمک می کند تا سریعاً نحوه ارزیابی داده ها را تعیین کنید.
اگر به خواندن GUM که تفاوت بین عدم قطعیت نوع A و نوع B را آموزش می دهد ادامه دهید،. گزیده زیر را خواهید دید.
3.3.5 واریانس تخمینی u که یک مؤلفه عدم قطعیت به دست آمده از ارزیابی نوع A را مشخص می کند، از یک سری مشاهدات مکرر محاسبه می شود و واریانس برآورد شده آماری آشنا s است. انحراف استاندارد تخمینی u، جذر مثبت u، بنابراین u = s است و برای راحتی، گاهی اوقات عدم قطعیت استاندارد نوع A نامیده می شود. برای یک جزء عدم قطعیت به دست آمده از ارزیابی نوع B، واریانس تخمینی u با استفاده از دانش موجود ارزیابی می شود، و انحراف استاندارد تخمینی u گاهی اوقات عدم قطعیت استاندارد نوع B نامیده می شود. – JCGM 100
از گزیده بالا، می توانید دو چیز را مشخص کنید.
- عدم قطعیت نوع A از یک سری مشاهدات محاسبه می شود،
- عدم قطعیت نوع B با استفاده از اطلاعات موجود ارزیابی می شود.
علاوه بر این، GUM اطلاعاتی در مورد توزیع احتمال برای هر نوع عدم قطعیت را در اختیار شما قرار می دهد.
بنابراین یک عدم قطعیت استاندارد نوع A از یک تابع چگالی احتمال حاصل از توزیع فرکانس مشاهده شده به دست می آید، در حالی که یک عدم قطعیت استاندارد نوع B از یک تابع چگالی احتمال مفروض بر اساس درجه به دست می آید. باور به اینکه یک رویداد رخ خواهد داد که اغلب به آن احتمال ذهنی می گویند. هر دو رویکرد از تفاسیر شناخته شده احتمال استفاده می کنند. – JCGM 100
عدم قطعیت نوع A با توزیع مکرر مشاهده شده مشخص می شود، به این معنی که برای یافتن توزیع احتمال صحیح باید به هیستوگرام نگاه کنید.
با پیروی از قضیه حد مرکزی، هر چه تعداد نمونه های بیشتری جمع آوری کنید، داده ها بیشتر شبیه یک توزیع نرمال می شوند.
از سوی دیگر، عدم قطعیت نوع B با استفاده از توزیع احتمال مفروض بر اساس اطلاعات موجود مشخص می شود. بدون داده های اصلی یا هیستوگرام، شما باید تعیین کنید که چگونه داده ها بر اساس منابع اطلاعاتی شما مشخص می شوند.
بیشتر اوقات اطلاعات زیادی به شما داده نمی شود. بنابراین، مردم معمولاً توزیع را مستطیلی فرض می کنند.
با این حال، راه های زیادی برای ارزیابی داده های عدم قطعیت نوع B وجود دارد که هیچ کس هرگز به آنها حتی در بهترین راهنما ها برای تخمین عدم قطعیت. اشاره نمی کند.
امروز، من قصد دارم همه چیزهایی را که باید در مورد عدم قطعیت نوع A و نوع B بدانید را پوشش دهم. برای مشاهده آنچه در این راهنما پوشش داده شده است، به لیست زیر نگاه کنید.
- عدم قطعیت نوع A چیست؟
- ارزیابی عدم قطعیت نوع A
- نمونه هایی از ارزیابی عدم قطعیت نوع A
- عدم قطعیت نوع B چیست؟
- ارزیابی عدم قطعیت نوع B
- نمونه هایی از ارزیابی عدم قطعیت نوع B
- تفاوت بین نوع A و نوع B عدم قطعیت
- نحوه انتخاب نوع A یا نوع B
عدم قطعیت نوع A چیست؟
با توجه به (VIM)، عدم قطعیت نوع A “ارزیابی یک جزء عدم قطعیت اندازه گیری با تجزیه و تحلیل آماری مقادیر کمیت اندازه گیری شده به دست آمده در شرایط اندازه گیری تعریف شده است.”

در راهنمای بیان عدم قطعیت در اندازه گیری (GUM)، ارزیابی عدم قطعیت نوع A به عنوان روش ارزیابی عدم قطعیت توسط تجزیه و تحلیل آماری مجموعه ای از مشاهدات تعریف شده است.
اساساً، عدم قطعیت نوع A داده هایی است که از یک سری مشاهدات جمع آوری شده و با استفاده از روش های آماری مرتبط با تحلیل واریانس (ANOVA) ارزیابی می شود.
بنابراین، اگر نمونه های مکرر از نتایج اندازه گیری مشابه را جمع آوری کنید و آن را با محاسبه میانگین، انحراف معیار و درجه آزادی ارزیابی کنید، جزء عدم قطعیت شما به عنوان عدم قطعیت نوع A طبقه بندی می شود.
ارزیابی عدم قطعیت نوع A
در بیشتر موارد، بهترین راه برای ارزیابی داده های عدم قطعیت نوع A، محاسبه:
- میانگین حسابی،
- انحراف معیار، و
- درجه آزادی
میانگین حسابی
هنگام انجام یک سری اندازه گیری های مکرر، می بایست مقدار متوسط مجموعه نمونه خود را بدانید.
اینجاست که معادله میانگین حسابی می تواند به شما در ارزیابی عدم قطعیت نوع A کمک کند. می توانید بعداً از این مقدار برای پیش بینی مقدار مورد انتظار نتایج اندازه گیری آتی استفاده کنید.
تعریف
عدد مرکزی مجموعه اعداد که با جمع کردن مقادیر با هم و سپس تقسیم تعداد کل کمیت ها محاسبه می شود.
معادله
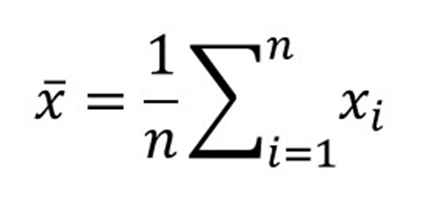
نحوه محاسبه
- همه مقادیر را با هم جمع کنید.
- تعداد مقادیر را بشمارید.
- مرحله 1 را به مرحله 2 تقسیم کنید.
انحراف معیار
هنگام انجام یک سری اندازه گیری های مکرر، همچنین می بایست میانگین واریانس مجموعه نمونه خود را بدانید.
در اینجا، شما می خواهید انحراف معیار را محاسبه کنید. رایج ترین ارزیابی نوع A است که در تحلیل عدم قطعیت استفاده می شود.
بنابراین، اگر فقط یک تابع برای یادگیری وجود داشت، این همان چیزی است که باید توجه شما را روی آن متمرکز کنید.
تعریف
اندازه گیری پراکندگی مجموعه ای از داده ها از میانگین آن (یعنی میانگین).
معادله
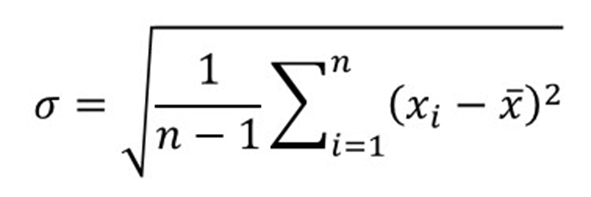
نحوه محاسبه
- هر مقدار را از میانگین کم کنید.
- هر مقدار را در مرحله 1 مربع کنید.
- تمام مقادیر مرحله 2 را جمع کنید.
- تعداد مقادیر را بشمارید و آن را از 1 کم کنید.
- مرحله 3 را به مرحله 4 تقسیم کنید.
- ریشه مربع مرحله 5 را محاسبه کنید.
درجه آزادی
پس از محاسبه میانگین و انحراف معیار، باید درجات آزادی مربوط به مجموعه نمونه خود را تعیین کنید.
این یک مقدار مهم است که اکثر مردم از محاسبه آن غفلت می کنند. حتی بیشتر راهنما های عدم قطعیت اندازه گیری فراموش می کنند که آن را در متن خود بگنجانند. با این حال، GUM ذکر آن را فراموش نکرده است.
در واقع، در بخش 4.2.6، GUM توصیه می کند که همیشه باید درجات آزادی را هنگام مستند سازی ارزیابی های عدم قطعیت نوع A لحاظ کنید.
موافقم.
من همیشه درجات آزادی را هنگام ارزیابی داده های نوع A و در بودجه های عدم قطعیت خود لحاظ می کنم.
همچنین می توانید از آن برای تخمین فواصل اطمینان و فاکتورهای پوشش استفاده کنید.
تعریف
تعداد مقادیری که در محاسبه نهایی یک آمار وجود دارد، متفاوت است.
معادله

نحوه محاسبه
- تعداد مقادیر موجود در مجموعه نمونه را بشمارید.
- مقدار مرحله 1 را به 1 کم کنید.
مثالی از ارزیابی عدم قطعیت نوع A
برای ارائه مثالی از ارزیابی داده های عدم قطعیت نوع A، می خواهم دو سناریوی رایج را که افراد هنگام تخمین عدم قطعیت اندازه گیری با آن مواجه می شوند، به شما نشان دهم.
- آزمون تکرارپذیری تک، و
- آزمون های تکرارپذیری چندگانه
آزمون تکرارپذیری واحد
تصور کنید که عدم قطعیت در اندازه گیری را تخمین می زنید و باید برخی از داده های نوع A را بدست آورید. بنابراین، شما یک آزمون تکرارپذیری انجام می دهید و یک سری اندازه گیری های مکرر را جمع آوری می کنید.
اکنون که داده ها را جمع آوری کرده اید، باید آن ها را ارزیابی کنید. بنابراین، شما میانگین، انحراف معیار و درجات آزادی را محاسبه می کنید.
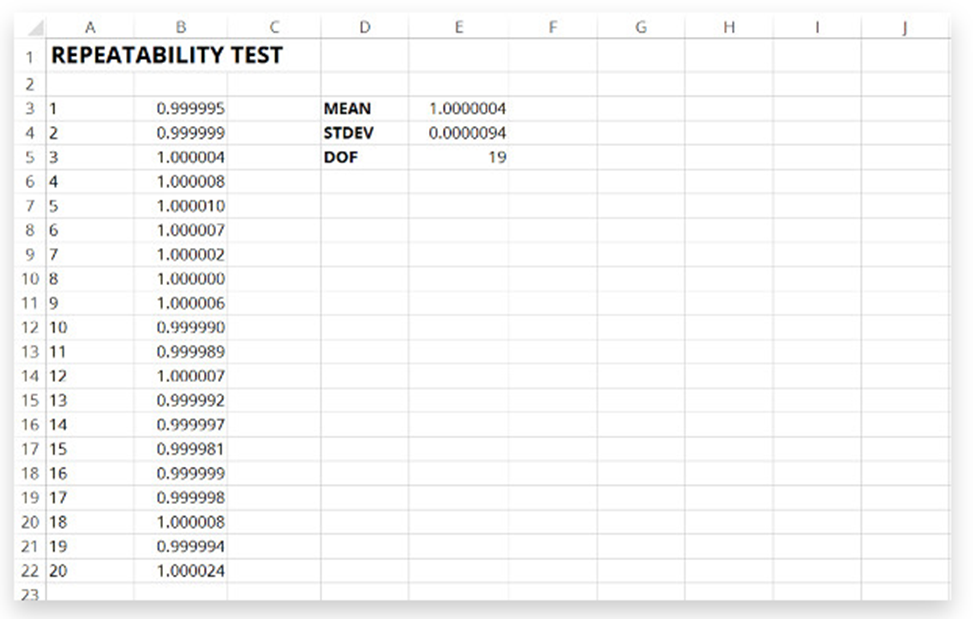
در مرحله بعد، انحراف استاندارد و درجات آزادی را برای تکرارپذیری به بودجه عدم قطعیت خود اضافه می کنید.
آزمون های تکرارپذیری چندگانه
در این سناریو، بیایید تصور کنیم که عدم قطعیت اندازه گیری را برای یک سیستم اندازه گیری که برای آزمایشگاه شما حیاتی است، برآورد می کنید. سعی کنید به استاندارد مرجعی فکر کنید که صاحب آن هستید.
بسیار مهم است که هر ماه یک آزمون تکرارپذیری برای این سیستم انجام دهید و نتایج را مستند کنید.

سوابق شما دارای میانگین، انحراف معیار و درجات آزادی ذکر شده برای هر ماه است.
با این همه داده نوع A، احتمالاً از خود می پرسید: “کدام نتایج را در بودجه عدم قطعیت خود لحاظ کنم؟”
پاسخ همه آنهاست. یا حداقل دوازده ماه گذشته.
برای ارزیابی داده های عدم قطعیت نوع A، باید از روش واریانس ادغام شده استفاده کنید. این روش بهترین راه برای ترکیب یا ترکیب انحرافات استاندارد شماست.
پس از انجام این تجزیه و تحلیل، می خواهید انحراف استاندارد ادغام شده نسبت به بودجه عدم قطعیت خود را برای تکرارپذیری محاسبه کنید.
عدم قطعیت نوع B چیست؟
با توجه به واژگان مترولوژی (VIM)، عدم قطعیت نوع B عبارت است از “ارزیابی یک جزء عدم قطعیت اندازه گیری که با ابزاری غیر از ارزیابی نوع A عدم قطعیت اندازه گیری تعیین می شود.”

در راهنمای بیان عدم قطعیت در اندازه گیری (GUM)، ارزیابی عدم قطعیت نوع B به عنوان روش ارزیابی عدم قطعیت با ابزاری غیر از تجزیه و تحلیل آماری مجموعه ای از مشاهدات تعریف شده است.
اساساً عدم قطعیت نوع B داده هایی است که از هر چیزی غیر از آزمونی که توسط شما انجام شده است جمع آوری می شود.
حتی اگر بتوانید داده ها را به صورت آماری تجزیه و تحلیل کنید، اگر آن ها را از یک سری مشاهدات جمع آوری نکرده باشید، داده های نوع A نیستند.
بیشتر داده های نوع B که برای تخمین عدم قطعیت استفاده می کنید، از آن ناشی می شوند.
- گزارش های کالیبراسیون،
- گزارش های آزمون مهارت،
- دستورالعمل های سازنده،
- جداول اطلاعاتی،
- روش های استاندارد،
- رویه های کالیبراسیون،
- مقاله های ژورنال،
- مقالات کنفرانسی،
- کاغذهای سفید،
- راهنماهای صنعت،
- کتاب های درسی، و
- سایر اطلاعات موجود.
ارزیابی عدم قطعیت نوع B
از آنجایی که عدم قطعیت نوع B می تواند از منابع بسیار متفاوتی باشد، راه های زیادی برای ارزیابی آن وجود دارد.
این بدان معنی است که اطلاعات زیادی برای پوشش دادن در این بخش وجود دارد.
بیشتر اوقات، افراد به طور پیش فرض توزیع مستطیلی را به یک جزء عدم قطعیت اختصاص می دهند و از جذر سه مقسوم علیه برای تبدیل کمیت ها به عدم قطعیت استاندارد استفاده می کنند.
خبر خوب این است که این مورد برای 90 درصد از محاسبات عدم قطعیتی که در طول زندگی خود انجام خواهید داد، کار خواهد کرد. با این حال، گزینه های واقعی تری برای ارزیابی عدم قطعیت نوع B در دسترس شماست.
بستگی دارد که بخواهید از آنها استفاده کنید یا نه.
اگر علاقه دارید به خواندن ادامه دهید. من قصد دارم روش های ارزیابی در GUM را پوشش دهم که اکثر راهنماهای عدم قطعیت اندازه گیری تمایل دارند آنها را کنار بگذارند.
“باید تشخیص داد که ارزیابی نوع B از عدم قطعیت استاندارد می تواند به اندازه ارزیابی نوع A قابل اعتماد باشد.”
مشخصات ساخت و گزارش های کالیبراسیون
در بخش 4.3.3 GUM، راهنما توصیه هایی برای ارزیابی اطلاعات منتشر شده در مشخصات سازنده و گزارش های کالیبراسیون ارائه می دهد.
«4.3.3 اگر تخمین xi از مشخصات سازنده، گواهی کالیبراسیون، کتابچه راهنمای یا منابع دیگر گرفته شده باشد و عدم قطعیت ارائه شده آن مضرب خاصی از یک انحراف استاندارد باشد، عدم قطعیت استاندارد u(xi) به سادگی همان عدم قطعیت ارائه شده است. مقدار تقسیم بر ضریب، و واریانس تخمینی مجذور آن ضریب است.

علاوه بر این، در بخش 4.3.4 GUM، راهنما اطلاعات بیشتری را برای ارزیابی مشخصات ساخت به شما می دهد.
4.3.4 عدم قطعیت ارائه شده xi لزوماً مانند 4.3.3 به عنوان مضربی از انحراف معیار داده نمی شود. درعوض، ممکن است دریافته شود که عدم قطعیت ارائه شده بازه ای با سطح اطمینان 90، 95 یا 99 درصد را تعریف می کند (به 6.2.2 مراجعه کنید). مگر اینکه خلاف آن مشخص شده باشد، می توان فرض کرد که یک توزیع نرمال (C.2.14) برای محاسبه عدم قطعیت نقل قول استفاده شده است و عدم قطعیت استاندارد xi را با تقسیم عدم قطعیت ارائه شده بر عامل مناسب برای توزیع نرمال بازیابی می کند. عوامل مربوط به سه سطح اطمینان بالا 1,64 است. 1,96; و 2,58 (همچنین به جدول G.1 در پیوست G مراجعه کنید).
اگر عدم قطعیت به یک بازه اطمینان خاص (به عنوان مثال 95٪) گزارش شود، از ضریب پوشش مرتبط برای تبدیل به عدم قطعیت استاندارد استفاده کنید.
در تصویر زیر گزیده ای از دیتا شیت Fluke 5700A است. باید توجه داشته باشید که مشخصات برای هر دو بازه اطمینان 95% و 99% بیان شده است.
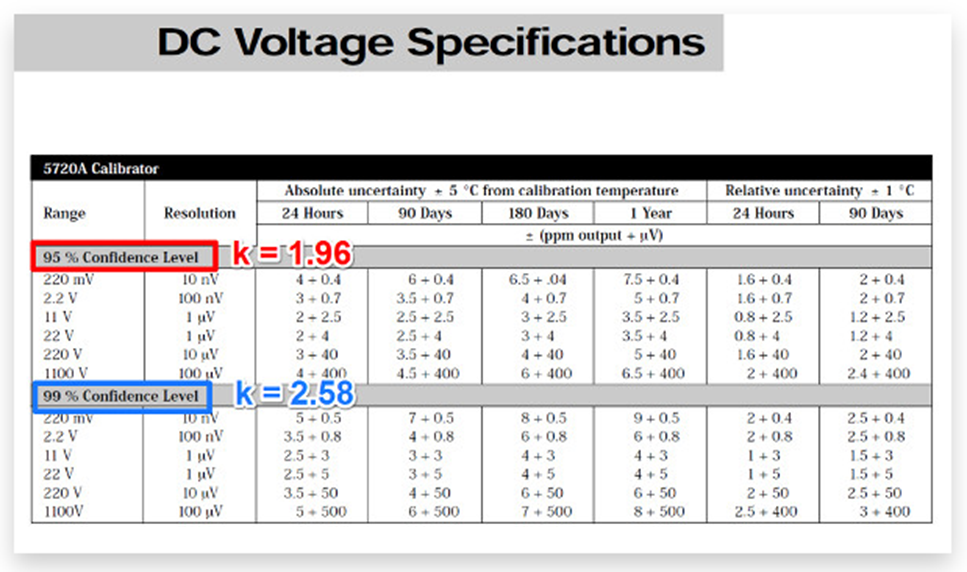
برای یافتن عدم قطعیت استاندارد، کافی است عدم قطعیت منتشر شده را بر ضریب پوشش (k) که با فاصله اطمینان ذکر شده در مشخصات مرتبط است، تقسیم کنید.
اگر سطح اطمینان در مشخصات ارائه نشده باشد (بیشتر اوقات ارائه نشده است)، بهتر است فرض کنیم که به فاصله اطمینان 95 درصد داده شده است. فقط در صورت اعلام فاصله اطمینان 99 درصد فرض کنید.
نکته حرفه ای: دفعه بعد که حسابرس شما پیشنهاد می کند که باید دقت یا عدم قطعیت مشخصات سازنده را با توزیع مستطیلی ارزیابی کنید، لطفاً آنها را برای خواندن بخش های 4.3.3 و 4.3.4 GUM ارجاع دهید.
50/50 احتمال وقوع
در بخش 4.3.5 GUM، راهنما به شما می گوید چگونه عدم قطعیت نوع B را زمانی که فکر می کنید احتمال وقوع 50 درصد وجود دارد، ارزیابی کنید. راهنما توصیه می کند که فاصله را بر 1.48 تقسیم کنید.
بنابراین، از معادله زیر برای تبدیل به عدم قطعیت اسکگتاندارد استفاده می کنید.
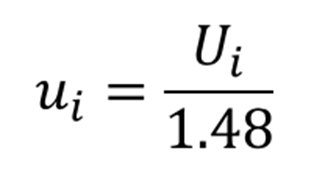
“4.3.5 موردی را در نظر بگیرید که بر اساس اطلاعات موجود، می توان گفت که “پنجاه درصد شانس وجود دارد که مقدار کمیت ورودی Xi در بازه a- تا a+ باشد” (به عبارت دیگر، احتمال اینکه Xi در این فاصله باشد 0.5 یا 50 درصد است. اگر بتوان فرض کرد که توزیع مقادیر ممکن Xi تقریباً نرمال است، بهترین تخمین xi از Xi را میتوان نقطه میانی بازه در نظر گرفت. بعلاوه، اگر نصف عرض بازه را با a = (a+ − a-)/2 نشان دهیم، می توان u(xi) = 1,48a را در نظر گرفت، زیرا برای توزیع نرمال با انتظار μ و انحراف استاندارد σ بازه μ ± σ /1,48 تقریباً 50 درصد از توزیع را در بر می گیرد.
اگر سر در گم هستید، نگران نباشید.
من هرگز با موقعیتی مواجه نشده ام که از این تکنیک برای ارزیابی عدم قطعیت نوع B استفاده کرده باشم. به احتمال زیاد، هرگز از آن استفاده نخواهید کرد مگر اینکه اندازه گیری هایی را انجام دهید که فقط دو نتیجه ممکن داشته باشد.
2/3 احتمال وقوع
در بخش 4.3.6 GUM، راهنما به شما می گوید که چگونه عدم قطعیت نوع B را در زمانی که فکر می کنید احتمال وقوع تقریباً 67 درصد وجود دارد، ارزیابی کنید. راهنما توصیه می کند که فاصله را بر 1 تقسیم کنید زیرا نزدیک به فاصله تحت پوشش یک انحراف استاندارد، 68.3٪ است.
بنابراین، از معادله زیر برای تبدیل به عدم قطعیت استاندارد استفاده می کنید.

4.3.6 موردی مشابه با 4.3.5 را در نظر بگیرید، اما در جایی که بر اساس اطلاعات موجود، می توان گفت که «حدود دو از سه احتمال وجود دارد که مقدار Xi در بازه a– تا a+ باشد. ” (به عبارت دیگر، احتمال اینکه Xi در این بازه قرار گیرد حدود 0.67 است). سپس می توان به طور منطقی u(xi) = a را در نظر گرفت، زیرا برای یک توزیع نرمال با انتظار μ و انحراف استاندارد σ، فاصله μ ± σ حدود 68.3 درصد از توزیع را در بر می گیرد.
مشابه احتمال وقوع 50/50، این یک ارزیابی معمولی نیست.
من هرگز با موقعیتی مواجه نشده ام که از این تکنیک برای ارزیابی عدم قطعیت نوع B استفاده کرده باشم. به احتمال زیاد، شما نیز هرگز از آن استفاده نخواهید کرد.
فقط حد بالا و پایین
در بخش 4.3.7 GUM، راهنما به شما می گوید چگونه عدم قطعیت نوع B را ارزیابی کنید، زمانی که فکر می کنید احتمال 100% وجود دارد که مقدار بین حد بالا و پایین باشد.
4.3.7 در موارد دیگر، ممکن است فقط بتوان کران های (حدود بالا و پایین) را برای Xi تخمین زد، به ویژه، بیان کرد که «احتمال اینکه مقدار Xi در بازه a- تا a+ برای همه موارد عملی باشد. برابر با یک است و احتمال اینکه Xi خارج از این فاصله باشد اساساً صفر است. اگر دانش خاصی در مورد مقادیر احتمالی Xi در این بازه وجود نداشته باشد، فقط می توان فرض کرد که به همان اندازه احتمال دارد که Xi در هر جایی در آن قرار داشته باشد (توزیع یکنواخت یا مستطیلی از مقادیر ممکن – به 4.4.5 و شکل 2 a مراجعه کنید. ). پسxi، انتظار یا مقدار مورد انتظار Xi، نقطه میانی بازه است، xi = (a- + a+)/2، با واریانس مرتبط…” است.
در این سناریو، راهنما توصیه می کند که یک توزیع مستطیلی تعیین کنید و فاصله را بر ریشه مربع 12 یا ریشه دوم 3 تقسیم کنید.

اگر انتظار می رود مقدار میانگین نقطه وسط بازه باشد، بر جذر 12 تقسیم کنید.

اگر اختلاف بین حدهای بازه معادل 2a باشد، بر جذر 3 تقسیم کنید.

اگر مطمئن نیستید که چگونه بازه را ارزیابی کنید، از معادله دوم استفاده کنید و بر جذر 3 تقسیم کنید. به احتمال زیاد روش ارزیابی صحیح است
حدود نامتقارن
هر چند وقت یکبار، ممکن است با مشخصات یا داده هایی مواجه شوید که به طور متقارن توزیع نشده اند. این بدان معنی است که حدود برای هر دو حد بالا و پایین برابر نیست.
“4.3.8 در 4.3.7، کران های بالا و پایین a+ و a- برای کمیت ورودی Xi ممکن است با توجه به بهترین تخمین xi متقارن نباشد. به طور خاص، اگر کران پایین به صورت a- = xi – b- و کران بالا به صورت a+ = xi – b+ نوشته شود، آنگاه b- ≠ b+. از آنجایی که در این مورد xi (فرض می شود که انتظار Xi است) در مرکز بازه a- تا a+ نیست، توزیع احتمال Xi نمی تواند در سرتاسر بازه یکنواخت باشد. با این حال، ممکن است اطلاعات کافی برای انتخاب توزیع مناسب وجود نداشته باشد. مدل های مختلف به عبارات مختلفی برای واریانس منجر می شوند. در غیاب چنین اطلاعاتی، ساده ترین تقریب…”
به عنوان مثال، حد بالایی می تواند فاصله بیشتری از حد اسمی نسبت به حد پایین داشته باشد. برای مشاهده مشخصات درجه 2 برای گیج بلوک مطابق با مشخصات GGG به تصویر زیر نگاه کنید.
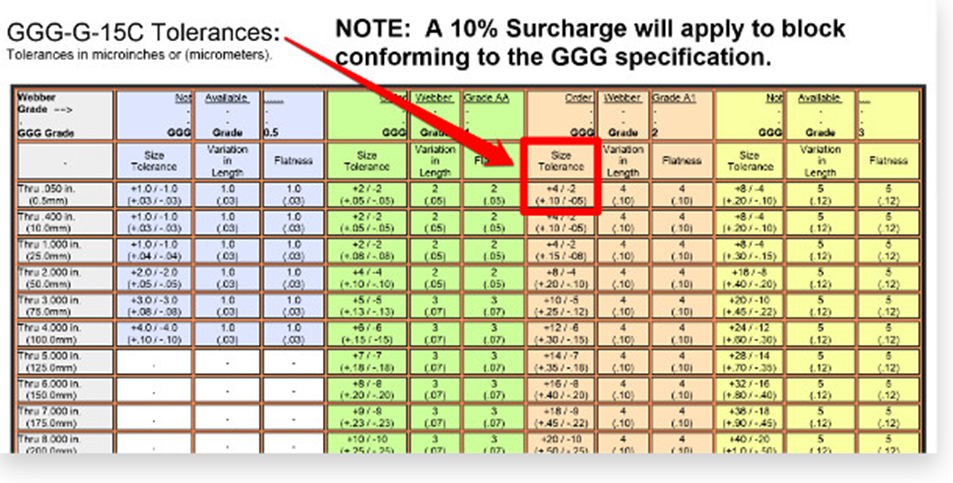
اگر توجه کنید، حد بالا و پایین از نظر قدر برابر نیستند. بنابراین، آنها نامتقارن هستند.
هنگامی که با این نوع سناریو مواجه می شوید، GUM دستورالعمل های زیر را برای ارزیابی عدم قطعیت نوع B توصیه می کند.

اگر حدود شما نامتقارن است، حد بالایی را بر حد پایین کم کنید و نتیجه را بر جذر 12 تقسیم کنید.

احتمال تساوی
حال، اگر یک یا دو چیز در مورد آمار بدانید، می دانید که توزیع مستطیلی زمانی استفاده می شود که همه شانس های وقوع به یک اندازه محتمل باشند.
با این حال، احتمالاً نمی دانستید که می توانید از توزیع مثلثی نیز استفاده کنید.
اگر این کار را کردید، عالی است. اگر نه، بخش 4.3.9 GUM را بخوانید.
«4.3.9 در 4.3.7، از آنجایی که هیچ دانش خاصی در مورد مقادیر احتمالی Xi در محدوده های تخمینی a- تا a+ وجود ندارد، تنها می توان فرض کرد که به همان اندازه احتمال دارد که Xi هر مقداری را در آن محدوده ها بگیرد. احتمال حضور در خارج از آنها صفر است. چنین ناپیوستگی های تابع مرحله ای در یک توزیع احتمال اغلب غیر فیزیکی هستند. در بسیاری از موارد، انتظار اینکه مقادیر نزدیک به مرز کمتر از مقادیر نزدیک به نقطه میانی باشند، واقع بینانه تر است. پس منطقی است که توزیع مستطیلی متقارن را با یک توزیع مثلثی متقارن با اضلاع شیبدار مساوی (یک ذوزنقه متساوی الساقین)، پایه ای با عرض a+ – a- = 2a، و بالای عرض 2aβ جایگزین کنیم، جایی که 0 <β <1. همانطور که β ← 1، این توزیع مثلثی به توزیع مستطیلی 4.3.7 نزدیک می شود، در حالی که برای β = 0، یک توزیع مثلثی است [به 4.4.6 و شکل 2 ب) مراجعه کنید. با فرض چنین توزیع مثلثی برای Xi، متوجه می شویم که انتظار Xi xi = (a- + a+)/2 است و واریانس مرتبط آن…”
GUM توضیح می دهد که توزیع مستطیلی همیشه واقعی نیست. اگر انتظار دارید مقادیر نزدیک تر به نقطه میانی و احتمال کمتری در حد رخ دهند، باید از توزیع مثلثی استفاده کنید.
علاوه بر این، حتی بینش بیشتری برای توصیه استفاده از توزیع مثلثی ارائه می دهد.

من فکر می کنم این ارزیابی عدم قطعیت نوع B بسیار جالب است. برای اکثر برنامه هایی که مردم معمولاً از توزیع مستطیلی استفاده می کنند، واقع بینانه و کاربردی است.
با این حال، من نمی بینم که اغلب از آن استفاده می شود و انتظار ندارم به این زودی شاهد تغییر بسیاری از مردم از توزیع های مستطیلی باشم.
برای کسانی که این کار را انجام می دهند، ممکن است از مزایای برآورد کوچکتر عدم قطعیت و سؤالات اضافی توسط ارزیابان خود بهره مند شوند. بنابراین، حتماً به این بخش از GUM مراجعه کنید تا با استفاده از آن از بودجه های عدم قطعیت خود دفاع کنید.
یکی دیگر از منابع خوب این مقاله توسط هوارد کاستروپ است. در پایین صفحه 15، هاوارد معادله جایگزین خوبی برای توزیع مثلثی به شما می دهد.

عدم قطعیت شمارش دوگانه
در تحلیل عدم قطعیت، دو مشکل رایج وجود دارد. عدم در نظر گرفتن منابع کافی عدم قطعیت در بودجه عدم قطعیت و مولفه های عدم قطعیت دوبار شمارش شده.
بخش 4.3.10 GUM به شما در مورد عدم قطعیت شمارش مضاعف هشدار می دهد تا از تخمین های اغراق آمیز عدم قطعیت اندازه گیری جلوگیری شود.
«4.3.10 مهم است که مؤلفه های عدم قطعیت را «دو بار شمارش» نکنید. اگر یک جزء عدم قطعیت ناشی از یک اثر خاص از ارزیابی نوع B به دست آید، باید آن را به عنوان یک جزء مستقل عدم قطعیت در محاسبه عدم قطعیت استاندارد ترکیبی نتیجه اندازه گیری تنها تا حدی که اثر کمکی نمی کند لحاظ شود. این کار به این دلیل است که عدم قطعیت ناشی از آن بخشی از تأثیر که به تغییرپذیری مشاهده شده کمک می کند، قبلاً در مؤلفه عدم قطعیت به دست آمده از تجزیه و تحلیل آماری مشاهدات گنجانده شده است.
من مؤلفه های عدم قطعیت دوبار شمارش شده را در تخمین های عدم قطعیت کالیبراسیون بسیار می بینم.
به عنوان مثال، یک آزمایشگاه یک واحد تحت آزمون«ایدهآل» (یعنی UUT) را برای ریزنگری UUT در تجزیه و تحلیل عدم قطعیت CMC خود در نظر می گیرد، سپس هنگام محاسبه عدم قطعیت کالیبراسیون، ریزنگری UUT واقعی را شامل می شود.
این دو شمارش است. و همیشه اتفاق می افتد.
حتی ارزیابان در مورد اغوا کردن آزمایشگاه ها برای شمارش مضاعف مؤلفه های عدم قطعیت در همان سناریویی که در مثال بالا ارائه شد، بعضی اوقات بد عمل می کنند.
در واقع، من این هفته با یک ارزیاب صحبت کردم که می خواست بداند چرا ریزنگری UUT در محاسبه عدم قطعیت CMC لحاظ نشده است. مجبور شدم با خوشحالی او را به خواندن بخش 5.4 از ILAC P14:01/2013 ارجاع دهم.
مثال رایج دیگر شمارش مضاعف زمانی است که یک آزمایشگاه شامل، اجزای عدم قطعیت است که معمولاً در مؤلفه های عدم قطعیت نوع A گنجانده می شوند. تکرارپذیری و تجدید پذیری
خبر بد این است که تعیین اینکه آیا یک جزء عدم قطعیت قبلاً در مؤلفه عدم قطعیت دیگری به حساب می آید می تواند دشوار باشد. این بدان معنی است که تقریباً غیرممکن است که از عدم قطعیت شمارش دوگانه جلوگیری کرد.
نمونه هایی از ارزیابی عدم قطعیت نوع B
ارزیابی داده ها از گزارش های کالیبراسیون
ارزیابی داده های گزارش های کالیبراسیون شما تا زمانی که کالیبراسیون های تایید صلاحیت شده ISO/IEC 17025 را دریافت کنید بسیار آسان است.
اکثر کالیبراسیون های تایید صلاحیت نتیجه اندازه گیری و عدم قطعیت اندازه گیری مرتبط را گزارش می کنند. علاوه بر این، گزارش سطح اطمینان عدم قطعیت تخمینی را به شما می گوید. به طور معمول، 95٪ که در آن k = 2.
بنابراین، تنها کاری که باید انجام دهید این است که عدم قطعیت گزارش شده را بر فاکتور پوشش (k) تقسیم کنید.
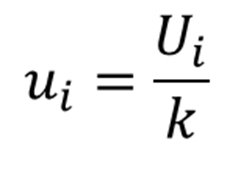
با استفاده از اطلاعات نشان داده شده در گزارش کالیبراسیون زیر و معادله داده شده در بالا، باید بتوانید عدم قطعیت گسترده را به عدم قطعیت استاندارد تبدیل کنید.

به سادگی عدم قطعیت گسترده (U) را بر فاکتور پوشش (k) تقسیم کنید. نتیجه شما عدم قطعیت استاندارد خواهد بود.

ارزیابی داده ها از مشخصات سازنده
ارزیابی داده ها از مشخصات سازنده به آسانی ارزیابی داده های گزارش های کالیبراسیون شما است.
به طور معمول، مشخصات سازنده را می توان در کتابچه های راهنمای سازنده، برگه های داده، کاتالوگ ها یا سایر مواد بازاریابی یافت.
با این حال، همه تولیدکنندگان هنگام انتشار مشخصات، دقت لازم را انجام نمی دهند. بنابراین، ممکن است مجبور شوید برخی فرضیات را مطرح کنید.
اکثر تولید کنندگان تایید صلاحیت شده، مشخصات را با فاصله اطمینان مرتبط منتشر می کنند. در تصویر زیر مشاهده می کنید که Fluke برای هر دو بازه اطمینان 95% و 99% مشخصات منتشر کرده است.

برای این مثال، اجازه دهید بر روی مشخصات 95 درصد تمرکز کنیم تا سیگنال 10 ولت را با استفاده از محدوده 11 ولت ارزیابی کنیم.
با نگاهی به مشخصات عدم قطعیت مطلق 1 ساله برای محدوده 11 ولت، عدم قطعیت برای 10 ولت تقریباً 38 میکرو ولت است.
با استفاده از اطلاعات نشان داده شده در مشخصات سازنده، از معادله زیر برای تبدیل عدم قطعیت گسترده به عدم قطعیت استاندارد استفاده کنید.

پس از آن، ارزیابی شما از عدم قطعیت نوع B باید تقریباً 19.4 میکرو ولت باشد.

اکنون، احتمالاً به این فکر می کنید که “اگر مشخصات تولید کننده فاصله اطمینان را نشان ندهد چه؟”
پاسخ این است که فرض کنید با فاصله اطمینان 95 درصد بیان شده است و آن را مشابه مثال بالا ارزیابی کنید. از مقادیر 2 یا 1.96 برای ضریب پوشش k استفاده کنید.
ارزیابی داده ها از راهنما ها، هندبوک، مقالات و مقالات
هنگام ارزیابی عدم قطعیت نوع B، همیشه به راحتی نمی توانید از داده های خود استفاده کنید.
اکثر آزمایشگاه ها زمان یا منابع لازم برای آزمون هر عاملی را که به عدم قطعیت در اندازه گیری کمک می کند، ندارند. بنابراین، می خواهید از داده های آزمایشگاه های دیگری که قبلاً کار را برای شما انجام داده اند، استفاده کنید.
بزرگترین چالش پیدا کردن داده هاست! شما باید مقداری زمان و تلاش برای انجام تحقیقات اختصاص دهید. برای آسانتر کردن موضوع، من قبلاً فهرستی از 15 مکان ایجاد کردهام که میتوانید منابع عدم قطعیت را پیدا کنید.
هنگامی که داده ها را پیدا کردید و آنها را برای فرآیند اندازه گیری خود قابل استفاده دانستید، می توانید آن را برای تجزیه و تحلیل عدم قطعیت خود ارزیابی کنید.
اکنون، می توانید داده های عدم قطعیت نوع B را از طرق مختلف ارزیابی کنید. با این حال، من روی موقعیتی تمرکز می کنم که در 90 درصد مواقع قرار است با آن مواجه شوید.
به طور معمول، اطلاعاتی را در یک راهنما، مقاله کنفرانس یا مقاله ژورنالی پیدا می کنید که داده هایی را بدون هیچ اطلاعاتی در مورد آن به شما می دهد.
بنابراین، شما به احتمال زیاد داده ها را با توزیع مستطیلی مشخص می کنید و از معادله زیر برای ارزیابی مولفه عدم قطعیت استفاده می کنید.

به عنوان مثال، تصور کنید که در حال تخمین عدم قطعیت برای اندازه گیری ولتاژ با یک مولتی متر دیجیتال هستید. شما در حال انجام تحقیقات هستید و به طور تصادفی به مقاله ای که توسط Keysight Technologies منتشر شده است برخورد می کنید که اطلاعات بسیار خوبی دارد که با فرآیند اندازه گیری که عدم قطعیت آن را برآورد می کنید مرتبط است.
بنابراین، تصمیم می گیرید که برخی از اطلاعات را در بودجه عدم قطعیت خود بگنجانید.
تصویر زیر گزیده ای از مقاله ای در مورد خطاهای کابل کشی سیستم و خطاهای اندازه گیری ولتاژ DC در مولتی متر دیجیتال است که توسط Keysight Technologies منتشر شده است. این شامل اطلاعاتی در مورد خطاهای EMF حرارتی است که می خواهید در بودجه عدم قطعیت خود لحاظ کنید.

جدول در تصویر دارای اطلاعات بسیار خوبی است که به شما در تعیین کمیت خطاهای EMF حرارتی کمک می کند، اما اطلاعات بسیار کمی در مورد منشا داده ها ارائه می دهد. بنابراین، بهتر است فرض کنیم که داده ها دارای توزیع مستطیلی هستند.
برای اتصال مس به مس با تغییر دمای 1 درجه سانتیگراد، خطای EMF حرارتی شما باید تقریباً 0.3 میکرو ولت باشد. برای تبدیل مولفه عدم قطعیت خود به عدم قطعیت استاندارد، مولفه عدم قطعیت را بر ریشه مربع سه تقسیم کنید.

از سوی دیگر، ممکن است داده هایی را در یک راهنما، مقاله کنفرانس یا مقاله ژورنالی بیابید که به طور معمول توزیع شده است یا قبلاً به عدم قطعیت استاندارد تبدیل شده است.
همه داده های نوع B را مستطیلی فرض نکنید، تخمین های عدم قطعیت خود را بزرگتر از حد فرض می کنید. به دنبال سرنخ هایی باشید که به شما در یافتن روش مناسب برای ارزیابی آن کمک کند.
به عنوان مثال، تصور کنید که در حال انجام تحقیقات هستید و به طور تصادفی به مقاله ای که در مجله تحقیقات NIST منتشر شده است، برخورد می کنید. مطالعهای که پیدا کردید دارای اطلاعاتی است که با فرآیند اندازه گیری که عدم قطعیت آن را تخمین می زنید مرتبط است.
بنابراین، تصمیم می گیرید که برخی از اطلاعات را در بودجه عدم قطعیت خود بگنجانید.
تصویر زیر گزیده ای از مقاله ای در مورد عدم قطعیت و کالیبراسیون ابعادی توسط تد دویرون است که در مجله NIST Journal of Research منتشر شده است. این مقاله شامل داده هایی برای تغییر شکل الاستیک بلوک های گیج کالیبره شده با مقایسه مکانیکی است که می خواهید در بودجه عدم قطعیت خود لحاظ کنید.
توجه داشته باشید که مقاله بیان می کند که داده ها به عنوان عدم قطعیت استاندارد گزارش شده است که در آن k=1 است.
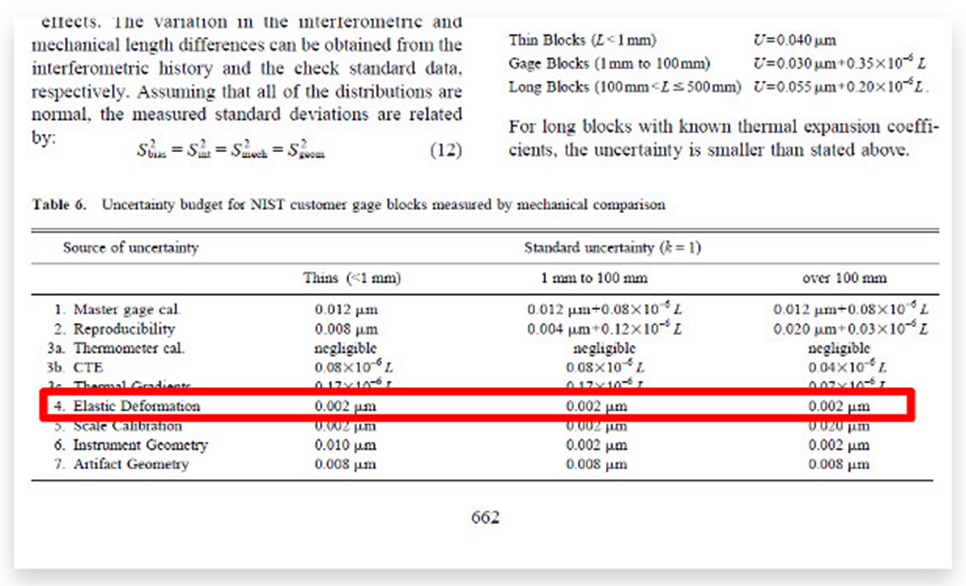
با فرض اینکه داده ها دارای توزیع نرمال و ضریب پوشش یک هستند، از معادله زیر برای ارزیابی عدم قطعیت نوع B استفاده کنید.
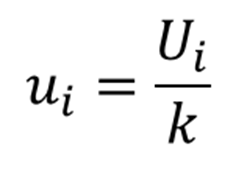
بنابراین، ارزیابی شما از عدم قطعیت نوع B باید تقریباً 2 میکرومتر باشد زیرا ضریب پوشش شما (k) یک است.

تفاوت بین عدم قطعیت نوع A و نوع B
اطلاعات غلط زیادی در مورد عدم قطعیت نوع A و نوع B وجود دارد.
تعاریف VIM دقیق ترین هستند. عدم قطعیت نوع A با استفاده از میانگین های آماری ارزیابی می شود. عدم قطعیت نوع B با استفاده از ابزارهای غیر از آماری ارزیابی می شود.
همه با روش های آماری ارزیابی می شود. بنابراین، تفاوت در نحوه جمع آوری داده ها است، نه نحوه ارزیابی آن ها.
عدم قطعیت نوع A از یک سری مشاهدات جمع آوری می شود. داده های نوع B از منابع دیگر جمع آوری می شود.
اگرچه عدم قطعیت نوع B یافت شده در نشریات ممکن است از یک سری مشاهدات جمع آوری شده باشد، اما توسط شما یا پرسنل آزمایشگاه شما جمع آوری نشده است.
بنابراین، مطمئن نیستید که داده ها از یک سری مشاهدات جمع آوری شده است. علاوه بر این، شما نمی دانید آزمون چگونه انجام شده است.
نتایج تجربی را می توان دستکاری کرد، به ویژه زمانی که توسط گروهی که می خواهند از نتایج سود ببرند (به عنوان مثال سازنده، آژانس حمایت شده و غیره)
در طول سال ها، بسیاری از محققان و آزمایشگاه ها در حال دستکاری آزمون ها برای دستیابی به نتایجی که به نفع خودشان یا مأموریتشان باشد، دستگیر شده اند. بنابراین، شما باید مراقب باشید.
تصویر زیر از phdcomics.com است. در مقطع کارشناسی ارشد هنگام پوشش موضوع اخلاق در تحقیق به من نشان داده شد. دستکاری واقع بینانه روش علمی را به تصویر می کشد.

نحوه انتخاب نوع A یا نوع B
بسیاری از مردم در تلاش برای تصمیم گیری در مورد عدم قطعیت نوع A یا نوع B مشکل دارند.
با این حال، لازم نیست که فرآیند دشواری باشد. در واقع، من یک فرآیند دو مرحله ای ساده را به شما نشان می دهم که به شما کمک می کند هر بار نوع عدم قطعیت صحیح را انتخاب کنید.
تنها کاری که باید انجام دهید این است که این دو سوال را از خود بپرسید.
سوال 1: آیا خودتان داده ها را از طریق آزمایش و آزمون جمع آوری کرده اید؟
- اگر بله، به سوال 2 بروید.
- اگر نه، نوع B را انتخاب کنید.
سوال 2: آیا سابقه اطلاعات شما بیشتر از 1 سال است؟
- اگر بله، نوع B را انتخاب کنید
- اگر نه، نوع A را انتخاب کنید
من حتی برای شما یک فلوچارت مفید درست کردم تا به شما کمک کنم تصمیم بگیرید که آیا داده های شما دارای عدم قطعیت نوع A هستند یا نوع B.
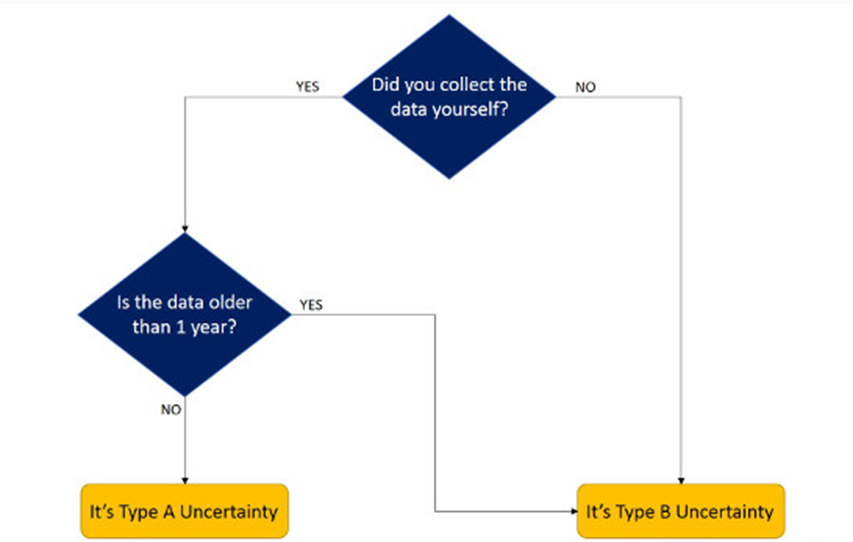
در مورد آن فکر کنید. اگر داده ها را خودتان جمع آوری کرده اید، آن گاه می خواهید آن را از نظر آماری ارزیابی کنید. بنابراین، داده نوع A است.
با این حال، اگر یک آزمون تکرارپذیری را 5 سال پیش انجام دادید و همچنان می خواهید بودجه عدم قطعیت خود را در آن لحاظ کنید، آنگاه داده های نوع B است.
سن داده ها مهم است. از این رو، دلیل سؤال دو است. شما باید به طور معمول داده های عدم قطعیت نوع A خود را به روز کنید.
اگر قدیمی تر از یک سال باشد، به احتمال زیاد داده های نوع B است و باید به زودی داده های بیشتری را جمع آوری کنید.
در حال حاضر، برخی از استثنا ها وجود دارد. من چندین روش تکرارپذیری را در طول سال ها مطالعه کرده ام که توصیه می کردند داده های دو ساله همیشه باید ثبت شوند.
با این حال، این روش مستلزم آن بود که داده های جدید باید هر ماه جمع آوری شود، به این معنی که سوابق آزمون شامل 24 رویداد نمونه گیری مستقل است. بنابراین، داده های جدید به طور مداوم جمع آوری می شد و به رکورد های تکرارپذیری اضافه می شد.
در این مورد، من آن را داده عدم قطعیت نوع A در نظر می گیرم.
در مورد انتخاب نوع عدم قطعیت استرس نداشته باشید، از دو سوال ذکر شده در بالا و بهترین قضاوت خود استفاده کنید. به شما کمک می کند تصمیم درستی بگیرید.
نتیجه
عدم قطعیت نوع A و عدم قطعیت نوع B دو طبقه بندی هستند که معمولا در تحلیل عدم قطعیت استفاده می شوند. معمولاً فقط برای مقاصد اطلاعاتی استفاده می شود، آنها به دیگران اطلاع می دهند که چگونه داده ها جمع آوری و ارزیابی می شوند.
این راهنما همه چیزهایی را که باید در مورد عدم قطعیت نوع A و B بدانید را پوشش داده است. این راهنما باید به شما کمک کند که تفاوت بین دو نوع عدم قطعیت را تشخیص دهید، بنابراین می توانید روش مناسب ارزیابی را برای تجزیه و تحلیل عدم قطعیت خود انتخاب کنید.
بنابراین، از اطلاعات استفاده کنید و برخی از این روش های ارزیابی را امتحان کنید. آنها باید به شما کمک کنند تا توانایی خود را برای محاسبه عدم قطعیت بهبود بخشید.
منبع:https://www.isobudgets.com
