نمودار ساقه و برگ

هیچ دو واحدی از محصول تولید شده توسط یک فرآیند یکسان نیستند. برخی از تغییرات اجتناب ناپذیر است. به عنوان مثال، محتوای خالص یک قوطی نوشابه از یک قوطی به قوطی دیگر کمی متفاوت است و ولتاژ خروجی منبع تغذیه دقیقاً از یک واحد به واحد دیگر یکسان نیست. آمار علم تجزیه و تحلیل داده ها و نتیجه گیری با در نظر گرفتن تنوع در داده ها است. چندین روش گرافیکی وجود دارد که برای جمع بندی و ارائه داده های x1، x2 بسیار مفید است. یکی از مفیدترین تکنیک های گرافیکی، دیسپل ساقه و برگ است. فرض کنید که داده ها با x1، x2 تا xn نشان داده شوند  و اینکه هر عددxi حداقل از دو رقم تشکیل شده است. برای ساختن یک نمودار ساقه و برگ، هر عدد xi را به دو قسمت تقسیم می کنیم: یک ساقه، که از یک یا چند رقم اصلی تشکیل شده است. و یک برگ، متشکل از ارقام باقی مانده. به عنوان مثال، اگر داده ها شامل درصد اطلاعات معیوب بین 0 تا 100 در بسیاری از ویفرهای نیمه هادی باشند، می توانیم مقدار 76 را به ساقه 7 و برگ 6 تقسیم کنیم. به طور کلی در مقایسه با تعداد مشاهدات باید ساقه های نسبتا کمی را انتخاب کنیم. معمولاً بهترین انتخاب بین 5 تا 20 ساقه است. هنگامی که مجموعه‌ای از ساقه‌ها انتخاب شد، در امتداد حاشیه سمت چپ نمایشگر فهرست می‌شوند و در کنار هر ساقه، تمام برگ‌های مربوط به مقادیر داده‌های مشاهده‌شده به ترتیبی که در مجموعه داده‌ها با آنها مواجه می‌شوند، فهرست می‌شوند. 

مثال 3.1

مطالبات بیمه سلامت

نسخه طرح ساقه و برگ تولید شده توسط Minitab گاهی اوقات طرح ساقه و برگ مرتب نامیده می شود، زیرا برگ ها بر اساس قدر مرتب شده اند. این نسخه از صفحه نمایش یافتن صدک داده ها را بسیار آسان می کند. به طور کلی، صدک 100 کیلومین مقداری است که حداقل 100 k٪ از مقادیر داده ها در این مقدار یا کمتراز این مقداراست.

و حداقل 100 (1 – k)٪ از مقادیر داده ها در این مقدار یا بالاتر از این مقدار است. صدک پنجاهم توزیع داده ها میانه نمونه نامیده می شود. میانه را می توان به عنوان مقدار داده ای در نظر گرفت که دقیقاً نمونه را به نصف تقسیم می کند، نیمی از مشاهدات کوچکتر از میانه و نیمی از آنها بزرگتراز میانه. اگر n، تعداد مشاهدات، فرد باشد، یافتن میانه آسان است. ابتدا مشاهدات را به ترتیب صعودی مرتب کنید (یا داده ها را از کوچکترین مشاهدات رتبه بندی کنید). سپس میانه مشاهده در موقعیت رتبه [(n – 1)/2 + 1] در این لیست خواهد بود. اگر n زوج باشد، میانه و میانگین مشاهده های رتبه بندی شده (n/2) و (n/2 + 1) است. از آنجایی که در مثال ما n = 40 یک عدد زوج است، میانه و میانگین دو مشاهده با رتبه 20و 21 است یا

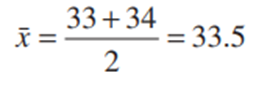
صدک دهم مشاهده با رتبه  4.5 = 0.5 + (0.1)(40) (نیمه راه بین مشاهده چهارم و پنجم) است.

یا 22= 2/(22 + 22) چارک اول مشاهده است.

فصل 3 ■ کیفیت فرآیند مدلسازی

با رتبه 10.5= 0.5 +(0.25) (40) (نیمه راه بین مشاهده دهم و یازدهم) یا26.5  = 2/(26 + 27) و چهارمین مشاهده با رتبه30.5 =0.5 +(0.75) (40) است (نیمه راه بین مشاهده سی و سی و یکم)، یا 39 = (37 + 41). ربع های اول و سوم گهگاه به ترتیب با نمادهای Q1 و Q3 نشان داده می شوند و محدوده بین چارکی IQR = Q3 − Q1  است که گهگاه به عنوان معیار تغییرپذیریبرای داده های خسارت بیمه استفاده می شود.

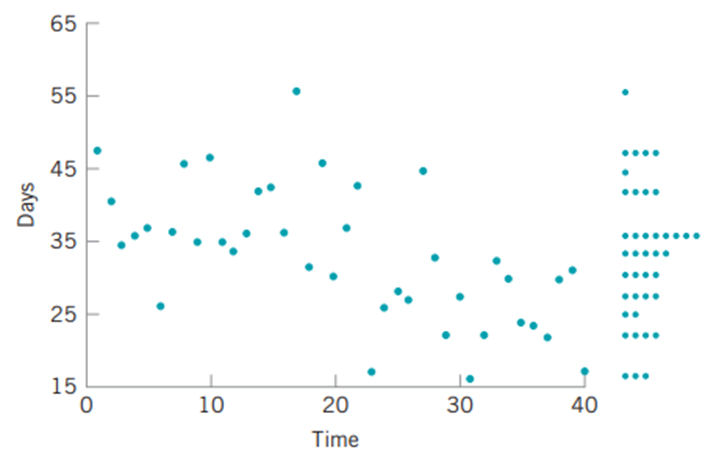
 محدوده بین چارکی IQR = Q3 – Q1=39 – 26.5 = 12.5  است. در نهایت، اگرچه نمایش ساقه و برگ یک راه عالی برای نمایش بصری تغییرپذیری در داده ها است، اما ترتیب زمانی مشاهدات را در نظر نمی گیرد. زمان ،اغلب عامل بسیار مهمی است که به تغییر در مشکلات بهبود کیفیت کمک می کند. البته می‌توانیم به سادگی مقادیر داده‌ها را در مقابل زمان رسم کنیم. چنین نموداری نمودار سری زمانی یا نمودار اجرا نامیده می شود. فرض کنید زمان چرخه رسیدگی و پرداخت مطالبات بیمه درمانی کارکنان در جدول 3.1 به ترتیب زمانی نشان داده شده. شکل 3.2 نمودار سری زمانی داده ها را نشان می دهد. ما از Minitab برای ساخت این نمودار (به نام نمودار حاشیه ای) استفاده کردیم و درخواست کردیم نمودار نقطه ای از داده ها در حاشیه محور y ساخته شود. این نمایشگر به وضوح نشان می دهد که زمان، منبع مهمی از تغییرپذیری در این فرآیند است. به طور خاص، زمان چرخه پردازش برای 20 ادعای اول به طور قابل توجهی بیشتر از زمان چرخه برای 20 ادعای آخر است. ممکن است چیزی در فرآیند تغییر کرده باشد (یا عمداً توسط پرسنل عملیاتی تغییر کرده باشد) که مسئول بهبود زمان چرخه است. بعداً در این کتاب، نمودار کنترل را به طور رسمی به عنوان یک تکنیک گرافیکی برای نظارت بر فرآیندهایی به این شکل و برای تولید یک سیگنال آماری در هنگام تغییر فرآیند معرفی می‌کنیم.

برای اطلاعات بیشتر میتوانید کتاب مونتکمری را مطالعه نمایید.