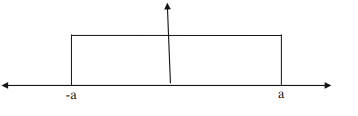
توزیع مستطیلی
برای تعریف توزیع مستطیلی اجازه دهید یک تابع احتمال (X)F را در نظر بگیریم که به صورت زیر تعریف شده است:

به این معنی که احتمال یافتن متغیر x در بین (-a) تا (+a) یکسان و برابر با 1/2a است. این تابع به عنوان تابع احتمال یکنواخت نیز نامیده می شود. اگر مقداری از پارامتر معینی از یک شی در تلورانس ˙+_a باشد، بدیهی است که مقدار واقعی پارامتر در هر جایی در محدوده (-a) تا (+a) با احتمال مساوی قرار دارد. یعنی پارامتر تابع احتمال مستطیلی است.
مقدار پارامتر همراه با یک محدوده خاص بیان می شود. هیچ اطلاعات دیگری در مورد ماهیت مقدار بیان شده، روش اندازه گیری یا به دست آوردن نصفه گستره داده نشده است. در آن صورت، میتوانیم با خیال راحت فرض کنیم که احتمال وجود مقدار بیانشده در هر جایی در محدوده بیانشده برابر است. کمی بعد میبینیم که چگونه میتوان عدم قطعیت استاندارد را از نیمهمحدودهی دادهشده محاسبه کرد.
یک آزمایشگاه اندازهگیری، پارامتری از یک ابزارخاص را کالیبره میکند و گواهیای صادر میکند که مقدار پارامتر و عدم قطعیت اندازهگیریها را بیان میکند. آزمایشگاه کاربر ابزار فرض میکند که مقدار اعلامشده ممکن است بین حدود عدم قطعیت با احتمال مساوی قرار داشته باشد. به عنوان مثال، جرم یک کیلوگرم استاندارد جرم (وزن) 1000.0025 گرم با عدم قطعیت ˙0:0001 گرم بیان می شود. در صورت عدم وجود هرگونه اطلاعاتی مبنی بر اینکه مقدار ذکر شده از کدام توزیع احتمال پیروی می کند یا روش بدست آوردن نیمه محدوده، آزمایشگاه کاربر ممکن است فرض کند که جرم واقعی استاندارد جرم ممکن است بین 1000.0024 و 1000.0026 گرم باشد. شانس مقدار بیان شده جرم در هر جایی بین محدوده های بیان شده یکسان است. با در نظر گرفتن میانگین به عنوان مبدا، توزیع مستطیلی مانند شکل زیر به نظر می رسد.

واریانس تابع مستطیل شکل
ما می دانیم که واریانس 2 یک تابع احتمال در موارد میانگین صفر به دست می آید

در این مورد، به عنوان میانگین صفر است x2 نشان دهنده مجذور انحرافات از میانگین است. بنابراین، واریانس 2 توسط رابطه


بنابراین عدم قطعیت استاندارد، که برابر با انحراف معیار است، برای با مقدار زیر است

