تابع عملکردی و مقادیر ورودی

در تابع عملکردی، کمیت های ورودی X1، X2، X3، …، Xn خود کمیت های اندازه گیری شده هستند که ممکن است بیشتر به کمیت های دیگر از جمله اصلاحات و عوامل تصحیح برای اثرات سیستماتیک بستگی داشته باشند، در نتیجه منجر به یک رابطه عملکردی پیچیده می شود، که اگر غیرممکن نباشد ممکن است دشوار باشد. به صراحت می توان گفت علاوه بر این، ممکن است تابعی از نظر جبری تعریف نشده باشد و ممکن است بخشی از آن به صورت تجربی تعیین شده باشد یا فقط به عنوان یک الگوریتم که به صورت عددی محاسبه می شود وجود داشته باشد. گاهی

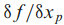
به صورت تجربی با اندازه‌گیری تغییر در Y و با گنجاندن تغییر در Xp تعیین می‌شود. در این مورد، بخشی از آن به ترتیب به بسط تجربی مرتبه اول تیلور تقلیل می یابد. بنابراین تابع f را می توان به معنای وسیع تری در نظر گرفت.

اگر مدل ریاضی درجه دقت مورد نظر را برآورده نکند، ممکن است مقادیر ورودی اضافی در تابع f گنجانده شود تا عدم کفایت برطرف شود.

به عنوان مثال برای توزین روزانه معمولی در یک بازار، جرم کالا به عنوان جرم اسمی وزن در نظر گرفته می شود. برای دقت بهتر، جرم واقعی وزن را در نظر می گیریم. برای دقت بهتر اصلاح شناوری هوا را اعمال می کنیم که ممکن است چگالی هوا را در نظر بگیریم
به صورت 1:2 کیلوگرم در متر مکعب. برای دقت بهتر، مقادیر چگالی هوا و وزن و قلم را با اندازه گیری ها محاسبه می کنیم. برای بهبود بیشتر دقت، ممکن است دوست داشته باشیم ترکیب واقعی هوا را بدانیم یا چگالی هوای داخل ترازو را فقط در زمان وزن کردن اندازه گیری کنیم. در حالت اول یک رابطه ساده را داریم، در مورد دوم یک اصلاح به دلیل جرم وزن اعمال می شود، در حالت سوم شناوری هوا اضافه می شود، رابطه چگالی هوا با شرایط محیطی بیشتر اضافه می شود و چند اندازه گیری چگالی اضافه می شود. وزن و قلم باید گرفته شود. برای بهبود آزمایش برای تعیین چگالی هوا در محل انجام شده و در رابطه اضافه شده است.

در مثالی دیگر، توان تلف شده در یک مقاومت معین توسط داده می شود

برای بهبود درستی، تغییر مقاومت R با دما باید در نظر گرفته شود:

اگر وابستگی به دما و اندازه گیری دما در نظر گرفته شود، رابطه پیچیده تر و پیچیده تر می شود.

منبع : عدم قطعیت اندازه گیری