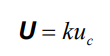
Measurement Uncertainty is a term that is used internationally to describe the quality of a measurement value. While this term has traditionally been reserved for many of the high accuracy measurements performed in metrology or gage laboratories, many customer and quality system standards require that measurement uncertainty be known and consistent with required measurement capability of any inspection, measuring or test equipment.
.In essence, uncertainty is the value assigned to a measurement result that describes, within a defined level of confidence, the range expected to contain the true measurement result. Measurement uncertainty is normally reported as a bilateral quantity. Uncertainty is a quantified expression of measurement reliability. A simple expression of this concept is:

U is the term for “expanded uncertainty” of the measurand and measurement result. Expanded uncertainty is the combined standard error (uc ), or standard deviation of the combined errors (random and systematic), in the measurement process multiplied by a coverage factor (k) that represents the area of the normal curve for a desired level of confidence. Remember, a normal distribution is often applied as a principle assumption for measurement systems. The ISO/IEC Guide to the Uncertainty in Measurement establishes the coverage factor as sufficient to report uncertainty at 95% of a normal distribution. This is often interpreted as k = 2.
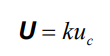
The combined standard error (uc ) includes all significant components of variation in the measurement process. In most cases, methods of
measurement systems analysis performed in accordance with this manual can be used as a tool to quantify many of the sources of measurement uncertainty. Often, the most significant error component can be quantified by

Other significant error sources may apply based on the measurement application. An uncertainty statement must include an adequate scope that identifies all significant errors and allows the measurement to be replicated. Some uncertainty statements will build from long-term, others short-term, measurement system error. However, the simple expression can be quantified as:

It is important to remember that measurement uncertainty is simply an estimate of how much a measurement may vary at the time of measurement.
It should consider all significant sources of measurement variation in the measurement process plus significant errors of calibration, master standards, method, environment and others not previously considered in the measurement process. In many cases, this estimate will use methods of MSA and GRR to quantify those significant standard errors. It is appropriate to periodically reevaluate uncertainty related to a measurement process to assure the continued accuracy of the estimate.
source : Analysis of measurement systems
